The signed and unsigned types in VHDL are bit vectors, just like the std_logic_vector type. The difference is that while the std_logic_vector is great for implementing data buses, it’s useless for performing arithmetic operations.
If you try to add any number to a std_logic_vector type, ModelSim will produce the compilation error: No feasible entries for infix operator “+”. This is because the compiler doesn’t know how to interpret this collection of bits that the vector is.
This blog post is part of the Basic VHDL Tutorials series.
We must declare our vector as signed or unsigned for the compiler to treat it as a number.
The syntax for declaring signed and unsigned signals is:
signal <name> : signed(<N-bits> downto 0) := <initial_value>;
signal <name> : unsigned(<N-bits> downto 0) := <initial_value>;Just like with std_logic_vector, the ranges can be to or downto any range. But declaring signals with other ranges than downto 0 is so uncommon, that spending any more time on the subject would only serve to confuse us. The initial value is optional, by default it’s 'U' for all bits.
We have already been using the integer type for arithmetic operations in previous tutorials. So why do we need the signed and unsigned types? For most, digital designers like to have more control of how many bits a signal actually uses.
Also, signed and unsigned values wrap around, while the simulator will throw a run-time error if an integer is incremented beyond bounds. Finally, signed and unsigned can have other values like 'U' and 'X', while integers can only have number values. These meta-values can help us discovering errors in our design.
Exercise
In this video we learn how signed and unsigned signals behave alike, and how they behave differently:
The final code we created in this tutorial:
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
entity T12_SignedUnsignedTb is
end entity;
architecture sim of T12_SignedUnsignedTb is
signal UnsCnt : unsigned(7 downto 0) := (others => '0');
signal SigCnt : signed(7 downto 0) := (others => '0');
signal Uns4 : unsigned(3 downto 0) := "1000";
signal Sig4 : signed(3 downto 0) := "1000";
signal Uns8 : unsigned(7 downto 0) := (others => '0');
signal Sig8 : signed(7 downto 0) := (others => '0');
begin
process is
begin
wait for 10 ns;
-- Wrapping counter
UnsCnt <= UnsCnt + 1;
SigCnt <= SigCnt + 1;
-- Adding signals
Uns8 <= Uns8 + Uns4;
Sig8 <= Sig8 + Sig4;
end process;
end architecture;
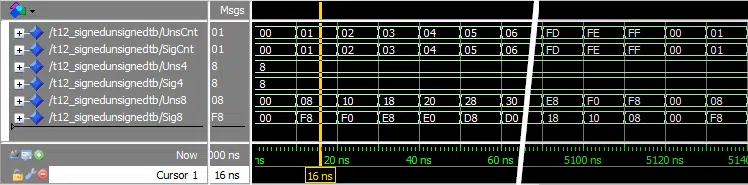
The waveform window in ModelSim, zoomed in on the interesting parts:
Analysis
The radix of all signals in the waveform are set to hexadecimal so that we can compare them equally.
In the wrapping counter example, we see that the signed and unsigned signals behave exactly the same way. Both UnsCnt and SigCnt start at 0, and are incremented one-by-one up to FF. Hex FF (decimal 255) is the largest value our 8-bit signals can hold. Therefore, the next increment wraps both of them back to 0.
We created the two 4-bit signals Uns4 and Sig4, and gave them both an initial value of “1000”. We can see from the waveform that they are both just hex 8 (binary 1000).
The last two 8-bit signals we created were Uns8 and Sig8. We can see from the waveform that their initial values are 0, as one would expect. But from there, they behave differently! Apparently, signed and unsigned types made a difference when adding two signals of different lengths.
This is because of something known as sign extension. Adding positive or negative numbers stored in vectors of equal length, is the same operation in digital logic. This is because of how two’s complement works. If the vectors are of different lengths, the shortest vector will have to be extended.
The unsigned 4-bit binary number “1000” is decimal 8, while the signed 4-bit number “1000” is decimal -8. The “1” at the left-most place of the signed number indicates that this is a negative number. Therefore, the two 4-bit signals are sign extended differently by the compiler.

This is a visualization of how sign extension creates the differing values for the Uns8 and Sig8 signals:

Get free access to the Basic VHDL Course
Download the course material and get started.
You will receive a Zip with exercises for the 23 video lessons as VHDL files where you fill in the blanks, code answers, and a link to the course.
By submitting, you consent to receive marketing emails from VHDLwhiz (unsubscribe anytime).
Takeaway
- Signals of signed and unsigned type are vectors that can be used in arithmetic operations
- Signals of signed and unsigned type will overflow silently
- Sign extension may create differing results for signed and unsigned types




I am confused by the article. To quote your text,
“The unsigned 4-bit binary number “1000” is decimal 8, while the signed 4-bit number “1000” is decimal -4”
Seems to me that “1000” in signed 2’s complement would be -8, not -4…right?
You are correct!
I changed the text to -8 now. Fortunately I said -8 in the video 🙂
Thank you for pointing that out.
Thank you Jonas very much for your informative article! Perhaps you could also comment on this approach?
With those in place we can do arithmetic and comparisons on std_logic_vectors directly. For example:
There is one disadvantage that all signals in the same file will be treated as signed or unsigned. Perhaps this approach is not the best way in any case.
Hi Andrew,
Your comment got me thinking about these packages. Even though I’ve been aware of them for quite some time, I don’t recall seeing them used in any projects which I have participated in. Why is that?
I believe this article by Sigasi sums up the main reason:
https://insights.sigasi.com/tech/deprecated-ieee-libraries/
The packages are vendor specific extensions, and not really part of the IEEE library.
Even though you save time by implicitly casting the std_logic_vector, I’m not convinced that it will be and advantage in the long run. It becomes difficult for other developers to jump in and understand what the code does.
You would have to look at the imports in the head of the file to see what your code line does. If the std_logic_unsigned is imported, the result may be something else than if std_logic_signed was used. I find it confusing, but that’s just my personal opinion.
Thank you Jonas, I agree with you.
Hello mr Jensen , thank you for all the materials which are huge help.
Got one question, How can we determine some bits of an unsigned signal?
for example:
But how about “0100”? is there any way to alter desired bits without writing the whole string?
Gets difficult when width of signals isn’t a small integer!
Sure, you can achieve that like this:
The range of values for signed 8 bit variable is given by the formula -2^(n-1) to 2^(n-1) – 1, n = 8
= -2^7 to 2^7 -1 = -128 to 127.
The range of values for unsigned 8 bit variable is given by the formula 2(^n) – 1, n = 8
= 2^8 -1 = 256.
For the counter of data type unsigned initialized to zero, the maximum count values is 0xff = 256
For the counter of data type signed initialized to zero, the maximum count value is 0x7f = 127
Do you agree?
Br, Lawrence
This statement is correct for signed types:
-2^(n-1) to 2^(n-1) – 1, n = 8 = -2^7 to 2^7 -1 = -128 to 127.
However, the range for unsigned will be 0 to 2^8 -1 = 255
(I’m sure you meant to write 255 and not 256 since you got the formula right).
VHDL signals always default to the leftmost value if you don’t initialize them. For std_logic, which is based on the enumerated type std_ulogic, this is the ‘U’ value.
However, the signed VHDL type is an array of std_logic’s. Therefore, the default initial value of a signed in VHDL isn’t a numeric value. It’s an array of ‘U’s.
Integers, on the other hand, behave as you were thinking the signed would. But the caveat is that it depends on which direction (to/downto) you gave the integer signal or variable when declaring it.
These are some examples of initial/default values:
-- Default values signal my_unsigned : unsigned(7 downto 0); -- "UUUUUUUU" signal my_signed : signed(7 downto 0); -- "UUUUUUUU" signal my_int1: integer range 0 to 255; -- 0 signal my_int2: integer range 255 downto 0; -- 255 signal my_int3: integer range -128 to 127; -- -128 signal my_int4: integer range 127 downto -128; -- 127I know it seems confusing, but it really isn’t. You just have to remember that the default initial value will always be the leftmost possible value of your type, regardless if it’s declared using “to” or “downto” direction.