Operator precedence in VHDL

VHDL groups operators into classes with different precedence levels. Operators are evaluated according to their classes, starting with the highest level. Operators of the same class don’t have any predefined priority. Instead, they are evaluated left to right in the order they appear in the code.

However, you can always use parentheses to force VHDL to calculate the sub-expressions in any order.

Operator precedence classes

This table shows VHDL’s operator classes listed from highest to lowest precedence.

Click the tabs below this text to switch between VHDL revisions!

The order of operators within a class in the table is arbitrary.

Note that the VHDL Language Reference Manual lists the operator classes in the opposite order. But in my opinion, listing higher priority classes at the top makes the most sense, as in the table above.

Precedence is almost entirely consistent throughout VHDL revisions, even as new language versions have introduced additional operators. The only exception is the transition from VHDL-2008 to VHDL-2019, which separates ** and abs not into separate classes.

Click the 2008 and 2019 tabs above the precedence table to see the difference!

Operators in the same precedence class

When encountering operators of the same precedence class, the sub-expressions will be evaluated from left to right. But that only applies to operators where such usage is allowed.

For example, this expression with only multiplication and division evaluates from left to right:

i <= 10 * 2 / 4; -- i = 5

And the same with multiple logical operators of the same type:

y <= '0' or '1' or '0'; -- y = '1'
 
y <= '0' and '1' and '0'; -- y = '0'
 
y <= '0' xor '1' xor '0'; --  y = '1'

But you cannot cascade multiple logical operators of different types without using parentheses:

y <= '0' nand '1' nor '0'; -- This will not compile!

Using parentheses

You can always use parentheses to enforce a custom evaluation order. The content of parentheses is calculated before the rest of the expression. If there are nested parentheses, the innermost is the first to evaluate.

To fix the example with multiple logical operators, we can use a set of parentheses around the NAND operation:

y <= ('0' nand '1') nor '0'; -- y = '0'

Or around the NOR operation if that’s what you wanted:

y <= '0' nand ('1' nor '0'); -- y = '1'

Using parentheses, you can also change the calculation order of mathematical expressions:

y <= 2 * 3 + 4; -- y = 10
 
y <= 2 * (3 + 4); -- y = 14

Some designers prefer always to use parentheses, even where it’s not strictly needed. That decision is up to you. Operator precedence in VHDL is 100% deterministic, but it doesn’t hurt to be explicit. It’s probably a good idea to add parentheses if you feel that it makes the code more readable.

Function calls in calculations

Function calls act as parentheses when used in VHDL expressions. Arguments are calculated before being passed to the function, and they return a value before other elements in the calling expression get evaluated:

  function add(a, b : integer) return integer is
  begin
    return a + b;
  end function;
   
begin
 
  y <= 2 * add(3, 2 + 2); -- y = 14

Unary and binary operators

Some unary operators have the same names as logical operators. They are similar but not the same and belong to different priority classes. Which one you use depends on whether you supply left- and right-hand arguments or only the left-hand argument.

The statement uses the unary OR operator:

sl <= or slv;

While this line selects the regular, binary OR operator:

slv <= slv_a or slv_b;

The result is different, and so is the precedence class of the operators.

A common pitfall of operator precedence

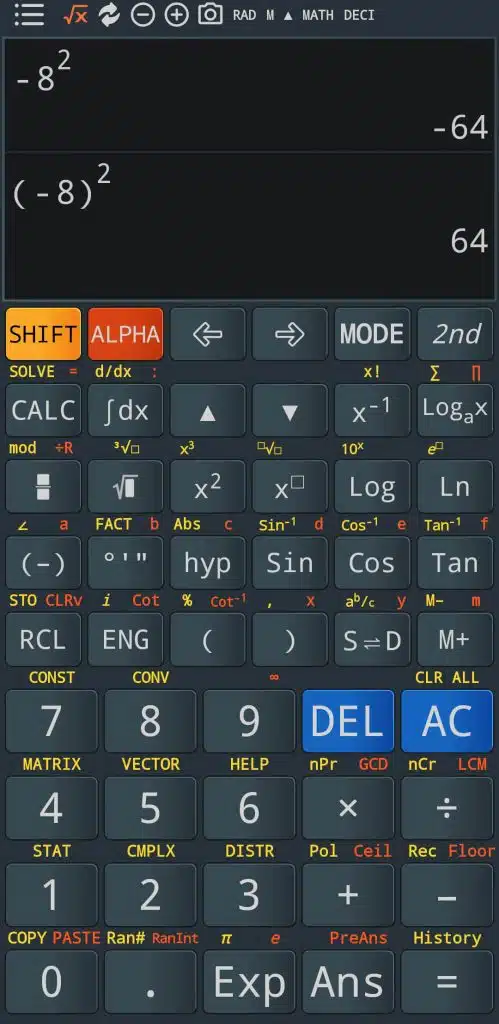
Finally, some common mistakes are associated with not correctly understanding operator precedence. For example, adding parentheses around the -8 number in the code below dramatically changes the result.

y <= -8**2; -- y = -64
 
y <= (-8)**2; -- y = 64

The explanation is that the exponential operator has higher precedence than the sign minus operator. Thus, 8**2 is calculated before the minus takes effect, and the result is -64. By putting -8 in parentheses, we override this behavior and get the square of -8, which is 64.

This behavior is in line with the most common practice regarding the order of operations in algebraic notation. You can easily reproduce the result in a scientific calculator, as shown below.