
VHDL has a built-in pseudo-random generator, but it can only generate floating-point numbers between 0 and 1. Fortunately, you can derive from this any other kind of random data format you should need. Continue reading this article to find out how to produce real or integer values of any range, as well as random std_logic_vector sequences and time values.
The uniform procedure from the IEEE MATH_REAL package is the basis for the algorithms described in this article. Please note that uniform relies on software to generate random numbers. Therefore, none of these algorithms are synthesizable. You can only use them in testbenches.
procedure UNIFORM(variable SEED1, SEED2 : inout POSITIVE;
variable X : out REAL);
The listing above shows the prototype of the uniform procedure. It needs two seed variables to work, and it will modify them every time you call the procedure. The output, X, is the random number, which always has a value between 0 and 1.
Just like other pseudo-random number generators, uniform will generate the same sequence of numbers when called with the same initial seed values. Because of this behavior, you can rerun the testbench and get the same result when using the same seed values.
Refer to the Efficient and Portable Combined Random Number Generators paper by Pierre L’Ecuyer for a detailed description of how this algorithm works. You can also view an actual implementation of the algorithm in the GHDL open-source VHDL simulator.
The test case
All of the examples in this article use the value 999 for both seeds. We declare the seed variables as listed below in the declarative region of a process. Then, we implement our custom randomization algorithms as impure functions within the same process.
variable seed1, seed2 : integer := 999;
You can download a complete testbench containing all the examples in this article by using the form below. The Zip file also contains a ModelSim project with a script that compiles and runs the simulation for you.
Random real value
The uniform procedure generates a random real value between 0.0 and 1.0. The real type is VHDL’s floating-point format. However, the chances are that you want the random number to be on a different range.
impure function rand_real(min_val, max_val : real) return real is
variable r : real;
begin
uniform(seed1, seed2, r);
return r * (max_val - min_val) + min_val;
end function;
Fortunately, we can easily translate the output from uniform by multiplying with a scale and adding an offset to it. The code above shows a function that returns a random real value within a min/max range.
Random integer value
To generate a random integer value within a specified range, you have to multiply by a scale and add an offset to it. But there is a pitfall that you have to avoid. You cannot simply generate a random real value within the range and round it to an integer.
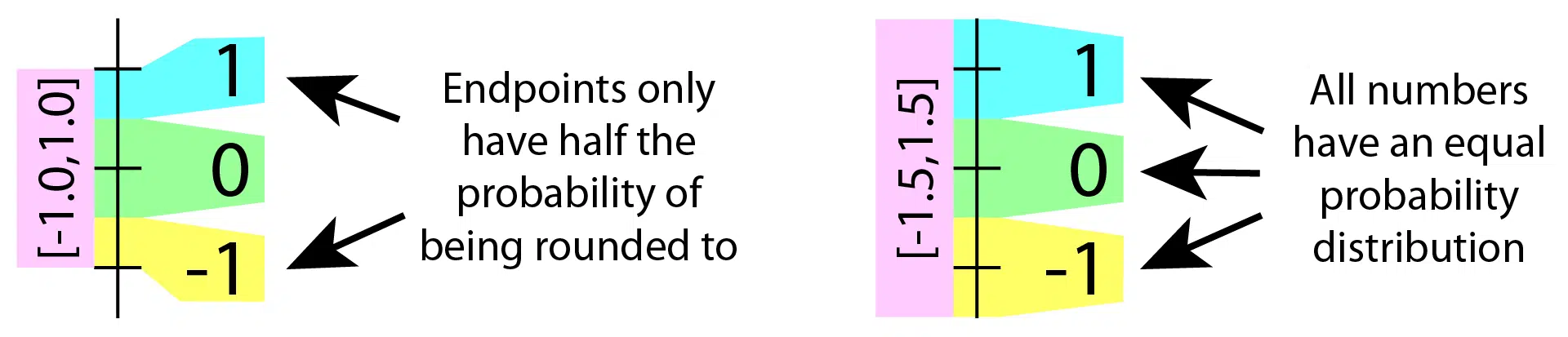
The illustration above shows the problem. In the example, we intend to generate a random integer value in the range -1 to 1. If we base our integer on a random real that goes precisely to the endpoints, the min and max integers only get half the probability of being chosen. Rounding to the 0 integer value happens half of the time, even though there are three number choices.
impure function rand_int(min_val, max_val : integer) return integer is
variable r : real;
begin
uniform(seed1, seed2, r);
return integer(
round(r * real(max_val - min_val + 1) + real(min_val) - 0.5));
end function;
In the code above, we correct for the endpoint rounding issue by adjusting the random real value to include an additional 0.5 above and below the endpoints.
Random std_logic_vector
There are many ways to fill a vector with random values, but this method works with vectors of any length. I’m using a for-loop to traverse the vector and select a random value for every bit. In the code below, the len parameter determines the length of the random std_logic_vector to return.
impure function rand_slv(len : integer) return std_logic_vector is
variable r : real;
variable slv : std_logic_vector(len - 1 downto 0);
begin
for i in slv'range loop
uniform(seed1, seed2, r);
slv(i) := '1' when r > 0.5 else '0';
end loop;
return slv;
end function;
Random time value
Sometimes you need to generate a random time value in your testbench. Perhaps you want to simulate an external interface which writes bursts of data at random times. Whatever the reason, random time values are easy to produce.
impure function rand_time(min_val, max_val : time; unit : time := ns)
return time is
variable r, r_scaled, min_real, max_real : real;
begin
uniform(seed1, seed2, r);
min_real := real(min_val / unit);
max_real := real(max_val / unit);
r_scaled := r * (max_real - min_real) + min_real;
return real(r_scaled) * unit;
end function;
To generate a random time value in VHDL, you must first convert the desired min and max values to real types. Then, after the randomization formula has done its magic, you convert the result back to a VHDL time type. Note that you must give the simulation time unit that you are using in the simulator as an argument to this function, as shown in the code above.
The OSVVM Random package
Finally, as an alternative to hand-crafting the randomization algorithm, you can use the Random package from the OSVVM library. It has multiple overloaded functions for generating random values for all kinds of VHDL types.
Open Source VHDL Verification Methodology (OSVVM) is a VHDL library for creating structured testbenches. The Random package is just one out of many useful packages in this library.
library osvvm;
use osvvm.RandomPkg.all;
The code above shows how to import the OSVVM package. ModelSim includes the library out-of-the-box, so you don’t have to download it for this simulator. Refer to the RandomPck.vhd file from the OSVVM GitHub repo to find a suitable randomization function for your needs.




Nice use of shared variables,
but VHDL 2008, needs all shared variables ot be of protected type,
so this code will at best raise warnings, at worse fail
can we have a version which uses protected types please
I avoided that problem in this article and downloadable code by using only regular variables. We placed the seed variables and all the new functions in the declarative region of a process.
If you want to share the randomization functions among multiple processes, you will have to define a package and create a shared variable from it. Then you can declare the seed variables and functions in the package.
I recommend studying OSVVM’s RandomPck.vhd to see how you can achieve that. Or simply just use OSVVM for that since it already has this excellent randomization package.
i’ve change a little the code, i have this:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; use ieee.math_real.all; use std.textio.all; entity random_gen_tb is port ( seed1_v : in std_logic_vector (7 downto 0); seed2_v : in std_logic_vector (23 downto 0); slv : out std_logic_vector(23 downto 0) ); end random_gen_tb; architecture arc of random_gen_tb is begin process variable seed1 : integer; variable seed2 : integer; variable l : line; subtype for_range is integer range 1 to 10; impure function rand_slv(len : integer) return std_logic_vector is variable r : real; begin seed1 := to_integer(unsigned(seed1_v)); seed2 := to_integer(unsigned(seed2_v)); for i in slv'range loop uniform(seed1, seed2, r); slv(i) <= '1' when r > 0.5 else '0'; end loop; return slv; end function; begin for i in for_range loop write(l, slv); writeline(output, l); end loop; wait for 0 ns; end process; end architecture;and when i synthesize it i obtain the following error: ERROR – CD371 :No matching overload for write
i dont know how to resolve this.
thank u in advance
I’m guessing you are trying to compile the file with VHDL-93′. Try VHDL-2008 or newer, and it should work.
If you use Questa/ModelSim: Project window->Right-click the file->Properties->VHDL-> Use 1076-2008.